ベイズ統計学の世界への誘い

はじめに

データイノベーション部の浅田です。

統計学のひとつにベイズ統計学というものがあります。ベイズ統計学は現代の機械学習において、重要な一角を占めています。

例えば、スパムメールかどうかを判定する機械学習の手法にナイーブベイズという手法があります。これはメールの文面に記載される単語について、スパムメールにその単語が出現する確率を学習しておき、判定対象のメールに書かれた単語から、そのメールがスパムメールかどうかを判定するような仕組みになっています。その際に、ベイズ統計学の根本をなすベイズの定理が使われています。

また、機械学習においては、パラメータの最適値を探す作業が度々発生します。例えば、ハイパーパラメータと呼ばれる人間が指定しなければいけない値がありますが、その値の最適値を探索する必要があったりします。そのような場合に、取りうるすべての値を試すのは時間がかかるので、効率的に探索する必要があります。そのような時に最適解に導く手法の一つに、ベイズ最適化というものがあり、その名の通りベイズ統計学の仕組みが使われています。

このように、機械学習についても重要なファクターであるベイズ統計学の理論についてご紹介したいと思います。

ベイズ統計学

ベイズ統計学では、確率は事象における直観的信頼度として表現されます。「事象の直観的信頼度」を平たい表現にすると、事象が起こると信じる度合い、と言えます。ベイズ的な考え方においては、信じる度合いとしての確率はデータ（確認された事実）によって変動します。その更新はベイズの定理によってなされるため、ベイズ更新と呼ばれます。

ベイズの定理

ベイズの定理は以下のような式になります。

\begin{aligned}P(H \mid D ) = \frac {P(D \mid H) \times P(H)}{P(D)} \end{aligned}

要素を分解してみましょう。$P$という記号は確率を表します。$P(H)$は$H$という事象が起こる確率と言う意味です。例えば、「真っ当な」サイコロであれば1が出る確率は$\frac{1}{6}$となるので、

\begin{aligned}P(サイコロで1が出る) = \frac{1}{6}\end{aligned}

となります。

$P(H \mid D)$は、条件つき確率と呼ばれるもので、$D$という条件が満たされた場合に$H$が起こる確率となります。

例えば、「真っ当な」サイコロで1が出る確率は先ほどの通り$\frac{1}{6}$となりますが、そこにサイコロの目が奇数だった、というデータ($D$)があらかじめ観測されたとします。そうすると、その条件の際に1になる確率は1,3,5のどれかに絞られるので、$\frac{1}{3}$となります。

つまり、

\begin{aligned}P(サイコロで1が出る \mid 出目が奇数) = \frac{1}{3}\end{aligned}

ということですね。

これをベイズの定理に当てはめてみましょう。

\begin{aligned} P(サイコロで1が出る \mid 出目が奇数 ) &=\frac {P(出目が奇数 \mid サイコロで1が出る) \times P(サイコロで1が出る)}{P(出目が奇数)}\\ &=\frac {1 \times \frac{1}{6}}{\frac{1}{2}}\\ &=\frac {1}{3} \end{aligned}

これは、ベイズ的な解釈をすれば「出目が決まっていない状態でサイコロの1の目が出ると信じていている確率である$\frac{1}{6}$が、出目が奇数であるという新たなデータを得たことで$\frac{1}{3}$に更新された(確信度があがった)」ということになります。これがベイズ更新の流れになります。

これだけだと回りくどいことをやっているように感じるかもしれませんが、ベイズの枠組みの面白いところは、この枠組みを主観的なパターンに応用できるところです。

イカサマサイコロ?

例えば、先ほどから「真っ当な」サイコロと表現していましたが、もし5回投げて5回とも1が出るという事実を目にした場合、このサイコロを真っ当なサイコロと思うでしょうか？5回も1が出たら「なにか変だぞ？」と思うのではないでしょうか。

その時の確信度の変化をベイズの定理でモデル化してみます。

\begin{aligned} P(イカサマ \mid 5回連続1が出る ) &=\frac {P(5回連続1が出る \mid イカサマ) \times P(イカサマ)}{P(5回連続1が出る)} \end{aligned}

この時、ベイズ統計では、

• $P(イカサマ \mid 5回連続1が出る )$を事後確率
• $P(5回連続1が出る \mid イカサマ)$を尤度(ゆうど)
• $P(イカサマ)$を事前確率
• $P(5回連続1が出る)$を周辺尤度

と表現します。

事前確率、事後確率、尤度、周辺尤度

ベイズの定理の再掲となりますが、

\begin{aligned}P(H \mid D ) = \frac {P(D \mid H) \times P(H)}{P(D)} \end{aligned}

ベイズ更新においては、上記の$P(H \mid D)$は「$D$という事象(データ)が観測された事後にHという事象が起こる確信度」となり、$P(H)$は「$D$という事象(データ)が観測されるよりも事前に$H$という事象が起こる確信度」となります。そのため、$P(H \mid D)$を事後確率、$P(H)$を事前確率と呼びます。ベイズ更新の枠組みでは、この事前確率を主観で決めてしまって構いません。なので、人間が事前知識として持っている確信度を当てはめてしまって問題ありません。データを観測することで、事前確率はデータを反映した事後確率に更新されることになります。

なお、ここまで$H$という文字を使っていましたが、これはHypothesis(仮説)の頭文字を表しています。事象$H$が起こる確信度とは、言い換えれば、事象$H$が起こるという仮説を信じる度合いと見なせます。つまりベイズ更新とは、観測されたデータによって仮説に対する確信度がどう更新されるか、ということをモデル化しているということになります。

事前確率がどのように事後確率に更新されるかは、$P(D\mid H)$と$P(D)$の比である$\frac {P(D\mid H)}{P(D)}$によって決まります。分子の$P(D \mid H)$を尤度（ゆうど）と呼びます。仮説$H$が正しいとした時にデータ$D$が観測される尤もらしさ、つまり「データが持つ仮説$H$に対する説得力」を表します。分母の$P(D)$は「データが一般的に観測される確率」で、周辺尤度などと呼ばれます。

$\frac {P(D\mid H)}{P(D)}$という値は$P(D \mid H)$が$P(D)$に比べて大きければ大きいほど値は大きくなります。言い換えると、データ$D$が一般的に観測される確率よりも事象$H$が起きた時にデータ$D$が観測される確率が高い事象であればあるほど大きくなります。したがって、観測されたデータ$D$が仮説$H$に対して固有であればあるほど、事前確率は確信度の高い事後確率に更新されることになります。

例えば、先ほどのイカサマサイコロの例であれば、5回連続1が出ることは真っ当なサイコロではレアケース=一般的にありえないであるため、イカサマがある時のほうが観測される確率が高いと判断されます。その結果、「イカサマサイコロかも」という思いはより確信度が高くなるでしょう。

続・イカサマサイコロ?

ベイズ統計モデリング

先ほどの5回連続で1が出た際に、「イカサマがあるんじゃないか？」と主観が変化することをベイズ統計を使ってモデリングしてみます。

今回は、

仮説$H$ =「サイコロで1が出る確率が6回に1回である」

とします。事前確率$P(H)$は仮説$H$に対する確信度ということになります。さて、その確信度をどう定義するかですが、ベイズ統計モデリングの特徴として、事前確率や事後確率を定義する際に確率分布を用いる点があります。

確率分布を用いることで、確率をより直観的に表現できます。

その確率分布に、α回成功してβ回失敗したときに、その成功確率pの分布を表現できるベータ分布というものがあります。

式の定義としては、

\begin{aligned} f(p;α,β) &=\frac {p^{α-1}(1-p)^{β-1}}{\int_0^1t^{α-1}(1-t)^{β-1}dt} \end{aligned}

となります。例えばα=5, β=5を指定すると、5回成功して5回失敗する場合の統計的な成功率の分布を表現することができます。式だけだと何ぞやって感じだと思いますので、ベータ分布をいくつか図示してみます。

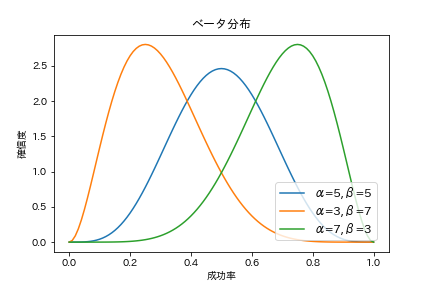
上図のように、α=5, B=5であれば成功率0.5付近が確信度が一番高くなっている形状になり、α=3, β=7だと成功率0.3付近が一番確信度が高くなっています。このようにして信頼度の分布を表現できるのが、確率分布を利用することによるメリットの一つです。なお、合計が10である必要はなく、任意の1以上の整数の組み合わせを指定できます。

ちなみに、α=5, β=5、α=10, β=10を指定した場合、成功率の確信度が高くなるのは0.5付近で同じですが、形状が少し異なります。

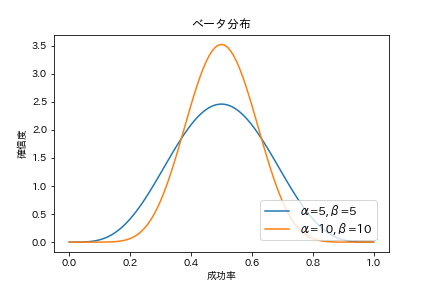
これはα=10, β=10のほうが「成功率が0.5付近であること」をより確信していることを表しています。なので、αとβの比は同じでも、合計数が大きくなればなるほど、成功率に対してより確信度が高い状態となります。これはデータが多ければ多いほど、真の値に近くという統計学の基本定理大数の法則とも合致します。

今回はこのベータ分布を事前確率として用います。今回のケースでは1が出ることを成功として定義して、1以外が出ることを失敗として定義すると、サイコロで6回に1が出る確率の分布を表現できます。今回は6回に1回ぐらい成功するはずだということで、α=2, β=10(12回投げて、2回は1が出て、10回はそれ以外が出る)としておきましょう。

なので事前分布$P(H)$は、以下のようになります。

\begin{aligned} f(p;2,10) &=\frac {p^{2-1}(1-p)^{10-1}}{\int_0^1t^{2-1}(1-t)^{10-1}dt} = \frac {p(1-p)^{9}}{\int_0^1t(1-t)^{9}dt} \end{aligned}

次に尤度です。尤度は仮説が正しいとした場合に、データが得られる確率です。つまり今回の場合、成功確率が6回に1回だったとして、5回中5回とも1の目が出る確率になります。このような時に使える分布として二項分布というものがあります。

\begin{aligned} f(k;n,p)=_n C _k p^k(1-p)^{n-k}=\frac{n!}{k!(n-k)!}p^k(1-p)^{n-k} \end{aligned}

この式で、kは成功回数、nは試行回数、pは成功確率となります。成功確率がpの時に、5回中5回成功する確率は、上記式に当てはめれば、

\begin{aligned} f(5;5,p)=\frac{5!}{5!(5-5)!}p^5(1-p)^{5-5}=p^5 \end{aligned}

となります。したがって$p^5$が今回の尤度です。

最後に、周辺尤度です。周辺尤度は尤度と事前確率分布との積であらわされる関数について全ての確率変数pを入力とした時の出力の合計値として算出されます。従って、事前確率分布の確率変数が取り得る値である0から1で関数を積分した値となります。

つまり、周辺尤度を式で表すと以下のようになります。

\begin{aligned} \int_0^1\frac {p(1-p)^{9}p^5}{\int_0^1t(1-t)^{9}dt}dp = \int_0^1\frac {p^{6}(1-p)^{9}}{\int_0^1t(1-t)^{9}dt}dp \end{aligned}

したがって求めるべき事後分布である$P(H \mid D)$は

\begin{aligned}P(H \mid D) =\frac {\frac {p^{6}(1-p)^{9}}{\int_0^1t(1-t)^{9}dt}}{\int_0^1\frac {p^{6}(1-p)^{9}}{\int_0^1t(1-t)^{9}dt}dp}\end{aligned}

…(´・ω・｀)

こんなの手で計算したくないですよね(少なくとも自分はやりたくありません)。ということで、python先輩にお任せします。

ここまでの計算をpythonのコードに落とし込むと、

import scipy.integrate as integrate


# 事前確率分布
p_h = lambda p: p * (1-p) ** 9 / integrate.quad(lambda t: t * (1-t) ** 9, 0, 1)[0]
# 尤度
p_d_h = lambda p: p ** 5
# 周辺尤度
p_d = integrate.quad(lambda p: p_d_h(p) * p_h(p), 0, 1)[0]
# 事後確率分布
p_h_d = lambda p: p_d_h(p) * p_h(p) / p_d

scipy.integrate.quad()は、第一引数の関数を、第二引数から第三引数の区間で積分してくれる関数です。結果は積分結果と誤差とのtapleになっています。なので、[0]を指定することで積分結果を取り出しています。

これで事後確率の確率分布が求まりました。事前確率の確率分布と尤度とともに図示して見ましょう。

import matplotlib.pyplot as plt
import numpy as np


# 確率変数
p = np.arange(0, 1.01, 0.01)
# グラフの準備
fig = plt.figure()
ax = fig.add_subplot(111)
plt.title("ベイズ更新")
plt.xlabel("成功率")
plt.ylabel("確信度")
# 事前確率分布
plt.plot(p, p_h(p), 'k--', color='g', label="事前確率")
# 事後確率分布
plt.plot(p, p_h_d(p), color='b', label="事後確率")
# 凡例
plt.legend(loc='lower right', borderaxespad=1, fontsize=12)
ax.twinx()
plt.ylabel("尤度")
# 尤度
plt.plot(p, p_d_h(p), 'k--', color='r', label="尤度")
# 凡例
plt.legend(loc='upper right', borderaxespad=1, fontsize=12)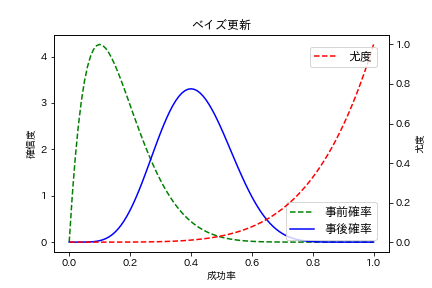

緑の破線で描かれている事前確率分布は0.15付近、つまりおよそ$\frac{1}{6}$付近の確信度が高くなっているのが見て取れます。これはデータを観測する前には、真っ当なサイコロで1が出る確率である$\frac{1}{6}$付近がサイコロで1の目が出る成功率だと信じていたことを示しています。

そして、赤の破線が尤度です。$\frac{1}{6}$付近の尤度は極めて低くなっています。ほぼ0です。これは5回連続で1の目が出ることは、1の目で出る成功率が$\frac{1}{6}$だとしたら、ほとんどありえないことを表します。

ベイズ更新の結果である、青の実線で描かれた事後確率分布では、成功率$\frac{1}{6}$付近の確信度はかなり下がっています。その代わり事前確率分布ではかなり確信度が低かった0.4以上の成功率に対する確信度が上がっています。つまり、データを観測した結果、成功率は$\frac{1}{6}$付近ではなく、もっと高い成功率なのでは？と考えるようになったことを表しています。

なお、今回のように確率分布における確率変数(今回の場合は成功率)が連続値である場合には、確率分布の関数を確率密度関数と言います。一方、二項分布などの場合には、確率変数が離散値となるので確率質量関数などと言います。確率密度関数においては、確率変数の値で積分をおこなうことによって、特定の確率変数の範囲における確率を計算することができます。例えば、今回のケースで言えば、サイコロの1の目が出る確率が0.4以上である確信度を計算することができます。

# 事前確率の0.4以上の成功率に対する確信度
print(integrate.quad(p_h, 0.4, 1)[0]) # 0.030233088000000016
# 事後確率の0.4以上の成功率に対する確信度
print(integrate.quad(p_h_d, 0.4, 1)[0]) # 0.5271741135912963

上記の結果から、0.4以上であることの確信度は0.03(=3%)から0.53(=53%)に跳ね上がったということになります。このようにピンポイントの確率変数だけでなく範囲を指定した確率変数に対する確信度を計算しやすい、というのも確率分布を使うメリットですね。

別解：scipy.statsにある確率分布を利用する

さて、上記では確率分布の定義式に、パラメータを当てはめて計算結果を求めたわけですが、pythonのscipyライブラリにあるstatsモジュールには様々な確率分布の計算を楽にしてくれる関数があります。

それを使うと先ほどの事後確率の計算は以下のようにも書けます。

import scipy.stats as st
import scipy.integrate as integrate


# 事前確率分布
p_h = lambda p: st.beta.pdf(p, a=2, b=10)
# 尤度
p_d_h = lambda p: st.binom.pmf(p=p, n=5, k=5)
# 周辺尤度
p_d = integrate.quad(lambda p: p_d_h(p) * p_h(p), 0, 1)[0]
# 事後確率分布
p_h_d = lambda p: p_d_h(p) * p_h(p) / p_d

scipy.stats.betaはベータ分布、scipy.stats.binomは二項分布を表します。beta.pdf()はベータ分布の確率密度関数を計算してくれる関数、binom.pmf()は二項分布の確率質量変数を計算してくれる関数になります。

上記の事前確率分布と尤度に使う組み合わせを変えてやれば、様々な確率分布を利用したベイズ更新に応用できます。

さらに別解：ベータ分布の性質の利用

なお、今回事前分布に利用したベータ分布は、尤度につかった二項分布と組み合わせた場合に、事後確率分布もベータ分布になります。尤度に対して、事前と事後の確率分布の種類が同じになる事前確率分布を共役事前分布と言ったりします。

そして、ベータ分布には便利な性質がもう一つあります。

それは、事前確率分布にベータ分布を使った場合、尤度にn回中k回成功した二項分布を使って事後確率分布を計算した結果と、事前確率分布のパラメータα, βに、それぞれ成功回数、失敗回数を追加したパラメータα+k, β+n-kを使って計算したベータ分布の結果とは一致するという性質です。

つまり、わざわざ二項分布をつかって尤度を計算したり、積分を行って周辺尤度を計算せずとも、事前確率分布のパラメータを調整するだけで、事後確率分布を得ることができます。

すなわち、今回のケースで求めた事後確率分布は以下のようにも求められます。

import scipy.stats as st


# 事前確率分布はα=2, β=10であり、
# 5回成功し、0回失敗したデータを観測したので
# αに2+5+7、βに10+0=10を指定する。
p_h_d = lambda p: st.beta.pdf(p, a=2+5, b=10+0)

事後確率分布は次のベイズ更新の事前分布として利用できる

以上でベイズ更新を使ってデータを観測した事後確率分布を求めることができました。そして、この事後確率分布はさらなるデータが観測された時の事前確率分布として使用できます。

つまり、さらにサイコロを振ったときにn回中k回1が出たデータを観測したのであれば、

import scipy.stats as st


p_h_d = lambda p: st.beta.pdf(p, a=7+k, b=10+n-k)

でさらなる事後確率分布を求められます。そのようにしてどんどんデータを集めていけば、その確信度を示す確率分布の密度は真の値付近に集中していきます。密度が集中している、つまり確信度が高いということは、データから判断するとその付近が求めたい値だと判断できるということです。

それがおよそ$\frac{1}{6}$に近づけば、そのサイコロは真っ当なサイコロであると判断できるでしょうし、それ以外の値に近づけば真っ当なサイコロではないと判断できるでしょう。

このような仕組みで、未知のパラメータを推定する手法をベイズ推定と呼びます。

おわりに

ベイズ統計学の世界の一端を垣間見ていただけたなら幸いです。冒頭でお伝えした機械学習に対する利用だけなく、ベイズ統計を利用することで回帰分析や仮説検定、時系列モデル分析など、様々な分析を行うことも可能です。またの機会にそれらについて、ご紹介できればと思います。

関連：ビジネスはAIの夢を見るか～AIがビジネスにもたらす価値～