バンディットアルゴリズムで複数案を効率的に評価！

はじめに

データイノベーション部の浅田です。

文章を書くときに、何度も構成や表現を練り直すことを推敲といったりします。この推敲という言葉は中国の故事に由来します。

唐代の賈島という詩人が詩を作っていた際に、「僧は推す月下の門」という句を考えつきますが、「推す」という表現を「敲く」という表現としたほうがいいのではないか、と迷い始めます。彼は考えに夢中になってるうち、韓愈というお偉いさんの行列に突っ込んでしまい咎められますが、韓愈が漢詩の大家だったので、「”敲く”のほうがいい」とアドバイスをもらうなど詩についておおいに語り合った、というのがこの故事の顛末です。

アイデア評価手法としてのA/Bテスト

詩を書くことはないにしても、ビジネスにおいても複数のアイデアを比較・評価するということはよくあります。

前述の賈島の例では、自分のセンスであったり、大家の意見を頼りにアイデアを評価したわけですが、統計学の力を借りてアイデアを評価することもできます。

例えば、Webサービスなどのデザインの比較・評価でよく利用される手法にA/Bテストというものがあります。これはA案とB案という二つのデザイン案があったとして、ユーザをランダムにA案、B案に振り分けて、そのデザイン案に対する反応を比較し、その結果どっちかの案が優れていると統計的に実証できれば、その案を全面的に採用する、というものです。

それをどう評価するかですが、二つの案を望ましい結果（たとえばクリック行動）を確率的に生み出すモデルとみなします。多数のユーザに対してランダムに提示して、その反応結果をデータとして集めることで、それぞれの案が望ましい結果を生み出す確率を推定し比較します。

どれぐらいデータを集めればいいのか

確率モデルのパラメータを推定するにあたって、一番確実なのはとにかくデータを集めることです。データを集めれば集めるほと、より正確なパラメータ、つまり望ましい結果を生み出す確率を推定することができます。

では、どれぐらいデータを集めればいいのでしょうか。100件？1000件？残念ながら、明確にこれだけあれば大丈夫という基準はありません。明らかに確率が違うなら100件でも十分なケースもあるでしょうし、どちらも甲乙つけがたいケースでは10000件でも十分ではないかもしれません。

問題になるのは件数だけではありません。データをたくさん集めればいいのは間違いないですが、データをたくさん集める、つまり長期間テストを実施するということは、ある一定のユーザには劣る案を提示し続けるということになります。例えば二つの案のうち、A案が改善案、B案が現状維持案であるとして、A案がより優れた案であったならばトータルとしてはB案だけでやっていた場合よりも良い結果になる可能性があるので、それほど問題にならないかもしれません。ただ、A案が実際には劣っている案だったとしたら、トータルの結果としては悪くなる可能性があります。つまり、続ければ続けるほど、損失が生まれる可能性があります。

多腕バンディット問題

そこで、複数の案を試す際に、なるべく損失を少ないように試すアルゴリズムとして、バンディットアルゴリズムというものがあります。

バンディットとは、ギャンブラーから金を奪い取る様子から盗賊に連想された「スロットマシン」の俗称です。複数のあたりの確率が異なるバンディット（スロットマシン）が存在する際に、どのように複数のアーム（レバー）を引けば得られる総額を最大化できるか、という問題を多腕バンディット問題と呼び、そのためのアルゴリズムがバンディットアルゴリズムになります。なので、多腕バンディットといっても、盗賊に腕がたくさん生えているわけではありません。

バンディットアルゴリズムの概念

バンディットアルゴリズムをイメージしやすくするために、こんな設定を考えてみましょう。

あなたは魔王を倒しにいく戦士です。魔王を倒すための武器を手に入れるため、武器屋に行きました。武器屋の主人に「この店で一番良い剣を買いたい」と伝えると、三つの剣を提示されました。武器屋の主人曰く「この三つの剣はどれも最強クラスの切れ味なんだが、時々しかその切れ味を発揮しない魔剣なんだ。切れ味を発揮すれば鉄だって簡単に切れる」ということです。

予算の都合上、三つの剣を全部買うことはできないので、切れ味を発揮する確率が一番高い剣を選ぶ必要があります。そこであなたは武器屋の主人にこう持ち掛けます。

「一回ごとに多少の料金を支払うから、それぞれの剣で試し切りをさせてほしい」

武器屋の主人は言いました。

「わかった。鉄を切れたら（切れ味を発揮できたら）、祝儀としてその回の試し切りの料金はタダでいい」

さて、この時に「切れ味を一番発揮しやすい剣をあまりお金をかけずに選び出すための戦略」というのがバンディットアルゴリズムとなります。

ε-greedy（イプシロングリーディ）アルゴリズム

バンディットアルゴリズムの筆頭格が、このε-greedyです。εはギリシャ文字でイプシロンと読みます。ここではεはある一定の小さい確率を意味します。

ε-greedyにおいては、

• εの確率でランダムに案を選びます。
• （1-ε）の確率で、それまでに得られたデータの平均値が最も高い案を選びます。

例えば先ほどの剣の例で説明すると、例えば10％の確率でランダムに剣を選んで試し切りを行います。そして、90％の確率でそれまでに一番鉄を切れた確率の高い剣を選んで試し切りを行います。

つまり、基本的には今まで試したなかで一番有望そうな案を試すけれども、一定確率において、別の案もランダムに試してみる、という戦略になります。

複数の案の中で優れた確率を持つ案があるのであれば、その案が大部分で選択されるように収束されるアルゴリズムです。

一方で、小さい確率とはいえ、ある一定確率で見込みがない案を最初から最後まで平等に試行してしまうアルゴリズムでもあります。

例えば、3回試した際に1回しか鉄を切れなかった剣Aと3回試した際に3回とも鉄を切れた剣Bがあった場合に、剣Aのほうはたまたま運が悪く、剣Bのほうはたまたま運が良かった可能性はあるので剣Aもまだ試す価値はありそうですが、もしこれが剣Aが100回中10回と剣Cが100回中50回という結果であれば、剣Aが剣Cよりも優れている可能性はあまりなさそうだと直感的に思うのではないでしょうか。

そのような時にもε-greedyは、平等に剣A, 剣B, 剣Cをランダムに選んでしまうので、結果が収束するのに時間がかかりますし、一定確率であまり見込みのない案を選んでしまいます。

トンプソンサンプリング

ε-greedyの問題点の一つは、複数の案を試す際にすべての案を常に平等に試そうとする点にあります。この問題点を改善するために、ベイズ統計の仕組みを利用したアルゴリズムがトンプソンサンプリングです。

ベイズ統計学についてはベイズ統計学の世界への誘いで記載したように、その特徴の一つとして確率モデルのパラメータを確率分布で表現します。

トンプソンサンプリングでは以下のような手順を踏みます。

1. 各案の確率モデルのパラメータを確率分布で表現します。
2. それぞれの確率分布から乱数を生成（サンプリング）します。
3. サンプリング結果のうち一番よい乱数を生成した確率分布をもつ案を次に試す案として採用します。
4. 得られた結果を使って、その案の確率分布をベイズ更新して事後分布を計算し、その案の新たな確率分布とします。
5. 2～４を繰り返します。

前述の記事において述べていますが、何回中何回成功したというデータを観測することにより、その成功確率をベータ分布という確率分布として表すことができます。

剣の例で言えば、各剣ごとに試行回数のうち何回鉄を切れたかのデータを観測することによって、鉄を切れる確率をベータ分布として表現できます。

確率分布が定義できれば、乱数をサンプリングすることができます。ミソとなるのは、期待値よりも大きい値がたまたま得られることも、期待値よりも小さい値がたまたま得られることもあり得ますが、確率的にあまりあり得ない値はサンプリングされにくいということです。

なので、「採用される案が偏る」という状態が発生するのは、それぞれの確率分布の期待値において統計的に有意差があるということでもあります。

このようにトンプソンサンプリングは、統計的に有望な案を効率的に試しつつ、損失を抑えるアルゴリズムとなっています。

コード例を挙げておきます。

from matplotlib import pyplot as plt 
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as st


class Sword:
    def __init__(self, p):
        self.p = p
        self.a = 0
        self.b = 0

    def slash_count(self):
        return self.a + self.b
        
    def slash(self):
        result = np.random.random() < self.p
        if result:
            self.a += 1
        else:
            self.b += 1
        return result
            
    def beta(self, x):
        return st.beta.pdf(x, a=self.a + 1, b=self.b + 1)
    
    def sampling(self):
        return np.random.beta(self.a + 1, self.b + 1)

    
class ThompsonSampling():
    def __init__(self, swords):
        self.swords = swords

    def _next_sword(self):
        samples = [sword.sampling() for sword in self.swords]
        return samples.index(max(samples))

    def do(self, counts):
        for _ in range(counts):
            self.swords[self._next_sword()].slash()


swordA = Sword(0.8)
swordB = Sword(0.5)
swordC = Sword(0.3)
swords = [swordA, swordB, swordC]

ThompsonSampling(swords).do(1000)

theta = np.arange(0, 1.01, 0.01)
plt.plot(theta, swordA.beta(theta), label="swordA")
plt.plot(theta, swordB.beta(theta), label="swordB")
plt.plot(theta, swordC.beta(theta), label="swordC")
plt.legend(bbox_to_anchor=(0, 1), loc='upper left', borderaxespad=1, fontsize=10)

# それぞれの剣を振った数
for sword in swords:
    print("振った数:{}, 鉄を切れた数: {}".format(sword.slash_count(), sword.a))

可視化で表示されたグラフは以下のようなものです。

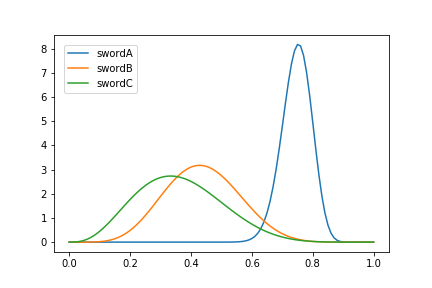
また、参考までに剣を振った数と鉄を切れた数は

剣A　振った数:77, 鉄を切れた数: 58  
剣B　振った数:14, 鉄を切れた数: 6  
剣C　振った数:9, 鉄を切れた数: 3

となっています。

一番確率の高い剣Aを一番多く試せていることがわかります。

試しに試行回数を1000回にした場合には

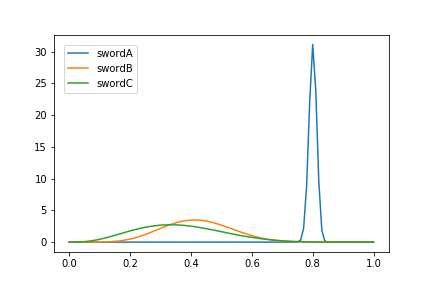
剣A　振った数:974, 鉄を切れた数: 780
剣B　振った数:17, 鉄を切れた数: 7
剣C　振った数:9, 鉄を切れた数: 3

となりました。有望案である剣Aの回数は増えている一方、それ以外の案の試行回数はほとんど増えていません。

終わりに

さて、トンプソンサンプリングのアルゴリズムによって、あなたは予算内に一番切れ味を発揮できた剣を選びだすことに成功し、感嘆の声をあげます。

「念願の魔剣を手に入れたぞ！」

この後どうなったかはご想像にお任せしますが、このようにバンディットアルゴリズムを使うことで、複数のアイデアを効率的に評価することが可能になります。ちなみに、バンディットアルゴリズムは強化学習において最適な方策を選択するためのアルゴリズムとしても使用されます。

なお、剣の例におけるトンプソンサンプリングでは、ほぼ一番有望な剣が選択されるように収束していますが、一番有望な剣でも鉄を切るのに失敗するケースが一定数存在します。なので、何も考えずにランダムに選択するケースや、ε-greedyに比べれば損失を少なくできていますが、さらに損失を少なくするためには、試行回数が十分であると判断した段階で打ち切る必要があります。試行回数が十分かどうかを判断するのはバンディットアルゴリズムの範疇を超えますが、一案としては、各案ごとの期待値に対して仮説検定を行って判断するといったことを行っても良いかと思います。仮説検定に関しては、またの機会にご紹介できればと思います。

以上、この記事が皆様の意思決定の一助にでもなれば幸いです。